|
Сопоставляя плановые суммы доходов и расходов, страховая организация определяет финансовый результат своей деятельности за определенный период, являющийся источником удовлетворения социально-экономических потребностей работников страховой компании, и ее дальнейшего развития.
Основу нормативного планирования составляет разработка страхового тарифа, позволяющего производить не только расчеты доходов и расходов по отдельным видам страхования, но и оценивать плановые отчисления на предупредительные мероприятия, ведение дела, получение прибыли и т. п.
Поскольку функционирование страховой организации представляет собой
динамическую систему, то для эффективного планирования ее деятельности применяется еще программно-целевое и экономико-математическое моделирование с использованием ЭВМ.
Прогнозирование страховых операций - важнейший элемент успешного развития страховых организаций в условиях рыночной экономики.
Прогноз - это вероятностная оценка будущего состояния страховой организации, основанная на статистических данных прошлого и настоящего уровней.
Цель прогнозирования - выявление главных тенденций и закономерностей в динамике страховых операций. Современной наукой достаточно подробно разработаны общетеоретические основы построения экономико-математических прогнозов с проведением расчетов на ЭВМ. С помощью экономико-математических прогнозов проводится анализ динамического ряда числа действующих договоров страхования в предпрогнозном периоде, а затем
методом экстраполяции
выявляется тенденция динамики. Далее с помощью экспертных оценок производится корректировка этой тенденции.
Доказано, что характер динамики экономических показателей страховой организации удается описать с помощью той или иной математической функции или аналитического управления. Подобрав соответствующее уравнение, на основе фактических данных исчисляют его параметры (постоянные коэффициенты). Исчислив параметры уравнения, производят выравнивание, или налаживание динамического ряда, изменяя в уравнении только временной параметр (t). Способы выравнивания детально разработаны математической статистикой.
Рассчитанные по уравнению и нанесенные на график значения показателей дают функциональную кривую, которая наглядно показывает тенденцию движения ряда. Экстраполируя эту кривую, получают прогноз на будущее.
Таким образом, основным условием достоверного прогнозирования является
правильный выбор уравнения для описания тенденции. Так, например, ряд проб и испытаний разнообразных кривых показал, что динамику числа действующих договоров страхования наиболее точно отражает уравнение логистической функции[9]:
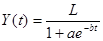 (7) (7)
где Y(t)- численность страхователей (число действующих договоров страхования);
L - предельное значение Y(t);
a, b - параметры (коэффициенты) уравнения, которые исчисляются, исходя из фактических значений динамического ряда за предпрогнозный период;
е - основание натурального логарифма, равное 2,718;
t - время, переменная величина, от изменения которой зависят конкретные годовые значения прогноза.
Графически логистические кривые похожи на латинскую букву "S" в силу чего их называют "S-образные кривые".
Остальные показатели (например, поступления страховых взносов, страховые выплаты и др.), посредством которых можно прогнозировать финансовые результаты страховых операций, определяются путем выявления корреляционных зависимостей, при помощи построения уравнений регрессии, отражающих зависимость поступлений взносов от изменения количества договоров страхования и доходов населения (поскольку сумма поступлений зависит от числа застрахованных и размера уплачиваемых каждым из них страховых взносов).
Объемы страховых выплат в прогнозируемом периоде могут быть определены
по уравнению регрессии, отражающему зависимость выплат от поступления страховых платежей. Аналогичным образом можно прогнозировать и расходы на ведение страховых операций. Затем
сальдовым методом определяются финансовые результаты.
Вначале строится так называемый точечный прогноз. Он показывает вероятные средние значения исчисляемых показателей. Прогноз достоверен, но в пределах определенных отклонений. Вероятная величина отклонений исчисляется как величина, пропорциональная среднему квадратичному отклонению с коэффициентом пропорциональности td, определяемым по распределению Стьюдента (числовые значения коэффициента Стьюдента (td) приводятся в специальных таблицах).
Перейти на страницу: 1 2 3 |